PCA与SVD

　　 最近接触到了PCA与SVD经过网上查找资料简单理解后，在此记录总结一下。

SVD

　　奇异值分解是一个有着很明显的物理意义的一种方法，它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要的特性。一个矩阵可以分解为两个方阵和一个对角矩阵的乘积。 对于一个M × N的矩阵A，我们想要分解成如下的形式：

　　其中，U称为左奇异矩阵，V称为右奇异矩阵， Σ 仅在对角线上有值，我们称它为奇异值，其他的元素均为0。每个矩阵的维度如下：

举个栗子，SVD用于图像压缩

原图：

一只可爱的猫咪

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image 
plt.style.use('classic')
img = Image.open('猫咪.jpg')
imggray = img.convert('L') # 转化成灰度图片
imgmat = np.array(list(imggray.getdata(band = 0)), float)# 转化成数组形式
imgmat.shape = (imggray.size[1], imggray.size[0]) # 更换数组形态(m,n)
u, d, v = np.linalg.svd(imgmat) #奇异值分解得到三个矩阵 u = (m,m) d = (m,n) v = (n,n)
print("u: ",u.shape," d: ",d.shape," v: ",v.shape)
for i in [5, 10, 15, 20, 30, 50, 100, 200, 374]: # 使用 多少个奇异值
    reconstimg = np.dot(u[:,:i] * d[:i], v[:i,:]) 
    #u = (m,i) d = (i,i) v = (i,n) 部分奇异值分解 A(m,n) = u(m,i) * d(i,i) * v(i,n)
    plt.imshow(reconstimg, cmap='gray')
    t = "n = %s" % i
    plt.title(t)
    plt.show()

分解得到的三个矩阵的维度：

d则是svd函数得到的奇异值，从大到小排序。

使用5个奇异值：

很模糊。

使用15个奇异值：

整体大致可以看清楚了

使用50个奇异值:

当使用50个奇异值时，已经和原图没有多大的差别了。所以，奇异值可以代表矩阵的信息，当奇异值越大时，它代表的信息越多。因此，我们取前面若干个最大的奇异值，基本就可以还原数据本身了。

PCA

　　 PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

定义

　　PCA是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

基本步骤以及代码实现

　　这里主要讲一下PCA的基本步骤以及代码实现，至于分析过程以及原理就不讲了，还没研究得那么深，，，

1. 对数据进行归一化处理。通常做法是去均值处理

   　　生成10个样本，每个样本拥有4个特征并做去均值处理

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

   import numpy as np test = [[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1], [2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9], [1.3, 2.3, 2.1, 0.8, 1.4, 1.2, 2.1, 0.4, 0.7, 2.7], [1.8, 0.5, 0.1, 1.8, 2.4, 4.2, 1.1, 0.4, 1.7, 0.7] ] test_mat = np.matrix(test).T test_mean = np.mean(test,axis=1)#axis=0表示按照列来求均值，如果输入list,则axis=1 m, n = np.shape(test_mat) avgs = np.tile(test_mean, (m, 1))#将avgs拉伸成(m,n) data_adjust = test_mat - avgs print(m,n) print(test_mat) print("每列的均值 :",test_mean) print(data_adjust)

   

2. 求特征协方差矩阵

   　　在概率论和统计中，协方差是对两个随机变量联合分布线性相关程度的一种度量。协方差大于0表示x和y若一个增，另一个也增；小于0表示一个增，一个减。如果x和y是统计独立的，那么二者之间的协方差就是0；但是协方差为0，并不能说明x和y是独立的。协方差绝对值越大，两者对彼此的影响越大，反之越小。其定义如下：

   

   ​ 对于多维随机变量，我们往往需要计算各维度两两之间的协方差，这样各协方差组成了一个 n × n的矩阵，称为协方差矩阵，它是一个对称矩阵。当X,Y是同一个随机变量时，X与其自身的协方差就是X的方差，可以说方差是协方差的一个特例。

   

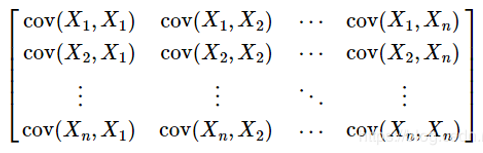
   对角线上的元素即为各维度上变量的方差。因为我们的数据拥有4的特征，所以协方差矩阵为[4,4]。

   1 2	covX = np.cov(data_adjust.T) #计算协方差矩阵 print("协方差矩阵为：\n",covX)

   

3. **求协方差的特征值和特征向量并将特征值按照从大到小的顺序排序 **

   1 2 3 4 5

   featValue, featVec= np.linalg.eig(covX) #求解协方差矩阵的特征值和特征向量 print("特征值为:",featValue) print("特征向量为:\n",featVec) index = np.argsort(-featValue) #按照featValue进行从大到小排序,并返回下标 print(index)

   

4. 将样本点投影到选取的特征向量上

   　　假设样本数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m * n)，协方差矩阵是n * n，选取的k个特征向量组成的矩阵为EigenVectors(n * k)。 将上面的n维特征变成k(k < n)维。

   1 2 3 4 5 6 7 8 9

   k = int(input("输入k的值")) if k > n: print("k的值应该小于n") else: #注意特征向量时列向量，而numpy的二维矩阵(数组)a[m][n]中，a[1]表示第1行值 selectVec = np.matrix(featVec.T[index[:k]]) #所以这里需要进行转置 finalData = data_adjust * selectVec.T print("原矩阵：\n",test_mat) print("投影后的数据: \n",finalData)

   k = 2：

   

   这样，就将原始样例的4维特征变成了2维，这2维就是原始特征在2维上的投影。