基于TensorFlow实现线性回归
深度学习
7 分钟 读完 (大约 1068 个字)

基于TensorFlow实现线性回归

线性回归模型简介

　　线性回归，就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候，就能够预测出一个简单的值，确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。


分析

　　这里使用了一个3层的神经网络，如下：

每层的权重以及偏差为：

1
2
3
4
5
6
7
8
9
10
11
12
13
#每层网络的权重
weights = {
    'w1': tf.Variable(tf.random_normal([1, 5])),
    'w2': tf.Variable(tf.random_normal([5, 3])),
    'out': tf.Variable(tf.random_normal([3, 1]))
}

#每层网络的偏差
biases = {
    'b1': tf.Variable(tf.random_normal([1, 5])),
    'b2': tf.Variable(tf.random_normal([1, 3])),
    'out': tf.Variable(tf.random_normal([1,1]))
}

生成测试数据

1
2
3
4
5
6
7
8
9
#生成训练数据 Training Data
#使用numpy生成200个随机点
x_data=np.linspace(-1,1,200)[:, np.newaxis]
b=np.random.normal(0,0.2,x_data.shape)
y_data=np.square(x_data)+b

#查看一下数据
plt.scatter(x_data,y_data)
plt.show()

数据分布如下图：


网络的搭建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def network(x, weights, biases):
    #网络第一层
    z1 = tf.add(tf.matmul(x, weights['w1']), biases['b1'])
    a1 = tf.nn.tanh(z1)  #使用tanh激活函数

    #第二层
    z2 = tf.add(tf.matmul(a1, weights['w2']), biases['b2'])
    a2 = tf.nn.tanh(z2)   #使用tanh激活函数

    #输出层
    z3 = tf.add(tf.matmul(a2, weights['out']), biases['out'])
    outputs = tf.nn.tanh(z3)
    return outputs
#定义损失函数
cost = tf.reduce_mean(tf.square(ys - outputs))
#优化函数(这里使用梯度下降法)
op = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

　　这里的拟合方法使用的是最小二乘法，它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。简单来说，就是求每个点到曲线的距离平方并相加，这样就得到一个损失值，然后使用梯度下降法优化它。使得它不断的减少，当到达一个临界点时即拟合完成。这里训练1000次，每100次输出当前损失值：

可以看出，当损失值到达0.04时梯度已经非常小了，这时候基本已经拟合。


未训练前


训练完成后

可以看出，经过训练已经拟合了。


完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

#每层网络的权重
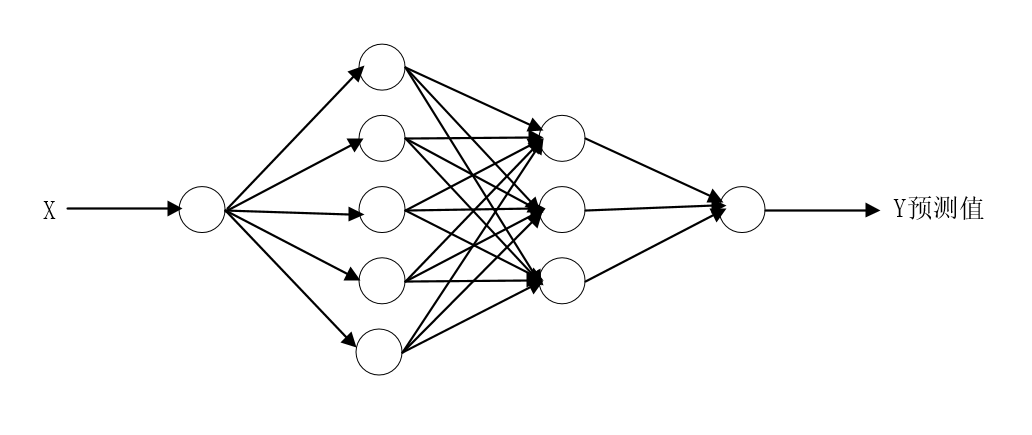
weights = {
    'w1': tf.Variable(tf.random_normal([1, 5])),
    'w2': tf.Variable(tf.random_normal([5, 3])),
    'out': tf.Variable(tf.random_normal([3, 1]))
}

#每层网络的偏差
biases = {
    'b1': tf.Variable(tf.random_normal([1, 5])),
    'b2': tf.Variable(tf.random_normal([1, 3])),
    'out': tf.Variable(tf.random_normal([1,1]))
}

#学习率
learning_rate = 0.1

#训练迭代次数
training_epochs = 1000
display_step = 100

#生成训练数据 Training Data
#使用numpy生成200个随机点
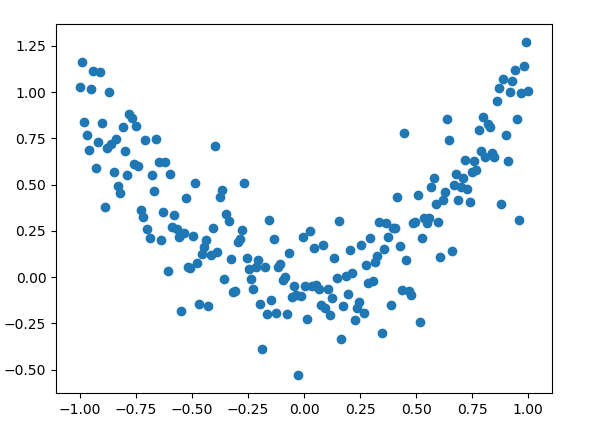
x_data=np.linspace(-1,1,200)[:, np.newaxis]
b=np.random.normal(0,0.2,x_data.shape)
y_data=np.square(x_data)+b

#查看一下数据
plt.scatter(x_data,y_data)
plt.show()

xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])

def network(x, weights, biases):
    #网络第一层
    z1 = tf.add(tf.matmul(x, weights['w1']), biases['b1'])
    a1 = tf.nn.tanh(z1)  #使用relu激活函数

    #第二层
    z2 = tf.add(tf.matmul(a1, weights['w2']), biases['b2'])
    a2 = tf.nn.tanh(z2)   #使用relu激活函数

    #输出层
    z3 = tf.add(tf.matmul(a2, weights['out']), biases['out'])
    outputs = tf.nn.tanh(z3)
    return outputs

if __name__ == "__main__":
    outputs = network(xs, weights, biases)
    #定义损失函数
    cost = tf.reduce_mean(tf.square(ys - outputs))
    #优化函数(这里使用梯度下降法)
    op = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
    #初始化
    init =tf.global_variables_initializer()

    #训练
    with tf.Session() as sess:
        sess.run(init)
        #未训练前
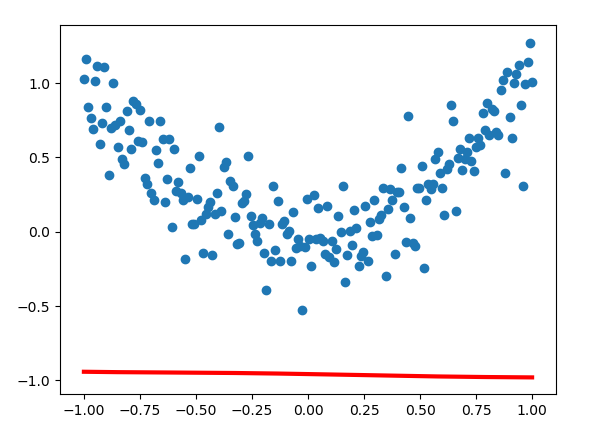
        Y1 = sess.run(network(xs, weights, biases), feed_dict={xs: x_data, ys: y_data})
        plt.scatter(x_data, y_data)  # 真实的散点值
        plt.plot(x_data, Y1, 'r-', lw=3)  # 预测值
        plt.show()
        #开始训练
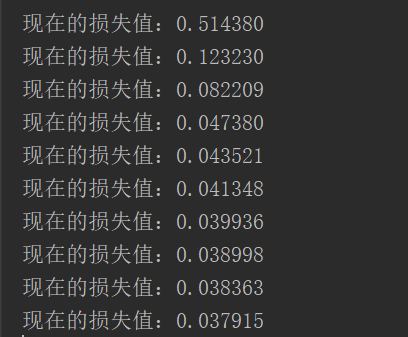
        for i in range(training_epochs):
            sess.run(op, feed_dict={xs: x_data, ys: y_data})
            if i%display_step == 0:
                print("现在的损失值：%f"%(sess.run(cost, feed_dict={xs: x_data, ys: y_data})))

        #获取预测的Y的值
        Y = sess.run(network(xs, weights, biases), feed_dict={xs: x_data, ys: y_data})

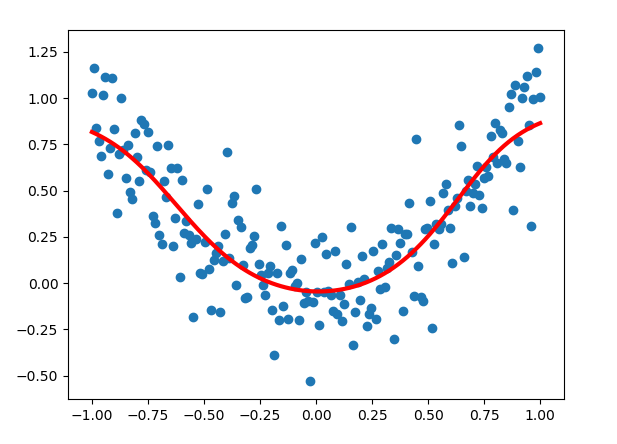
        plt.scatter(x_data,y_data) #真实的散点值
        plt.plot(x_data, Y, 'r-', lw=3)#预测值
        plt.show()

喜欢这篇文章？打赏一下作者吧

基于TensorFlow实现鸢尾花分类
深度学习-激活函数
关注我

链接

分类

标签云

C++ Python 爬虫

最新文章

归档

标签

C++ 4
Python 1
爬虫 1

最新文章

归档

标签

C++ 4
Python 1
爬虫 1
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×